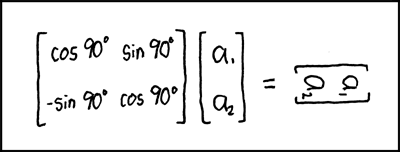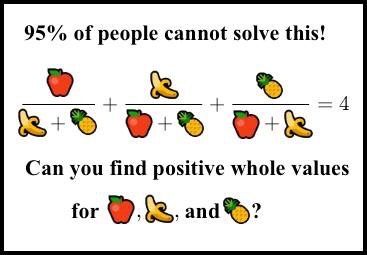MAT210 (Álgebra Lineal)

Departamento de Matemática, Universidad Técnica Federico Santa María (Valparaíso, Chile)

Profesor:

Pedro Montero
Oficina: F-247
Horario de consultas: Lunes a viernes de 8:00 a 17:00 previa coordinación por e-mail
Ayudantía: Juan Fuenzalida, Viernes de 14:00 a 15:30 (bloque 7-8)

Anuncios

Nuevo Examen Global: El Examen Global será el día Miércoles 12 de agosto de 9:00 horas a 21:00 horas. Los contenidos a evaluar serán las secciones $\S 1$ a $\S 43$.

Nuevo Información importante: Debido al reciente comunicado de Vicerrectoría Académica sobre el aplazamiento del fin del semestre en una semana, producto de la nueva semana de vacaciones del 22 al 29 de junio, es que les informo el nuevo calendario del curso para lo que resta de semestre (semana a semana):

Semana del 15 al 20 de junio: Clases normales lunes y miércoles. Certamen 2 el Sábado 20 de junio.
Semana del 22 al 27 de junio: Vacaciones.
Semana del 29 de junio al 4 de julio: Lunes sin clases. Miércoles clases normal. Viernes 3 de julio clase recuperativa (horario de ayudantia): link de Zoom será enviado por correo.
Semana del 6 al 11 de julio: Clases normales lunes y miércoles.
Semana del 13 al 18 de julio: Vacaciones de invierno.
Semana del 20 al 25 de julio: Lunes sin clases. Miércoles clases normal. Viernes 24 de julio clase recuperativa (horario de ayudantia): link de Zoom será enviado por correo.
Semana del 27 de julio al 1 de agosto: Clases normales lunes y miércoles. Quiz 3 el Viernes 31 de julio.
Semana del 3 al 8 de agosto: Clases normales lunes y miércoles. Certamen 3 el Sábado 8 de agosto.
Semana del 10 al 15 de agosto: Examen Global.

Se recomienda leer antes de la primera clase el siguiente documento que repasa contenidos de primer año. Ver aquí (Última actualización: 23/03/2020).

Pueden encontrar aquí una demostración del Teorema Fundamental del Álgebra (Argand, 1806)

Nuevo Nuevo: Pueden encontrar aquí un documento detallado sobre Formas Hermitianas.

Prerrequisitos

Se asumiran conocidos los contenidos de primer año. En particular, la operatoria básica de matrices aprendida durante el segundo semestre de primer año. Además, se supondra conocida la primera sección del documento anterior (correspondiente a contenidos del primer semestre de primer año): grupos, anillos y cuerpos, relaciones de equivalencia y cocientes, y la construcción del cuerpo $\mathbb{F}_p=(\mathbb{Z}/p\mathbb{Z},+,\cdot)$.

Consejo importante

Este curso es considerado desafiante para muchos estudiantes, pues es el primer curso donde se requiere y se evalúa el hacer demostraciones matemáticas. Recomiendo fuertemente leer antes de cada clase los apuntes de la sesión anterior, y luego de finalizar la clase releer los apuntes y escribir ejemplos explícitos lo más simples posibles de los conceptos discutidos.

Descripción

En esta asignatura los estudiantes se introducen en el estudio de los fundamentos del Algebra Lineal. Se profundizan tópicos como: resolución de sistemas lineales de ecuaciones; teoría de matrices; valores y vectores propios; herramientas matemáticas que han sido trabajadas durante el primer año. Concretamente, discutiremos sobre:

Recuerdo sobre espacios vectoriales y aplicaciones lineales $u:V\to W$.
Determinantes $\det(u)$, valores y vectores propios $u(v)=\lambda v$.
Endomorfismos diagonalizables, trigonalización, Cayley-Hamilton, espacios característicos.
Descomposición de Jordan $A=P^{-1}JP$, exponencial de matrices $\exp(A)$, espacios cocientes $V/W$.
Espacio dual $V^\ast=\mbox{Hom}_k(V,k)$. Formas bilineales simétricas y formas cuadráticas.
Espacios euclideanos y grupos ortogonales $\mbox{O}(n)$.
Formas hermitianas y grupos unitarios $\mbox{U}(n)$.
Aplicaciones multilineales y tensores.

La evaluación de este curso se realizará mediante 3 certamenes y 3 controles. Las fechas de estas evaluaciones son las siguientes:

Quiz 1 (Q1): Sábado 2 de mayo. Contenidos a evaluar: $\S 1$ a $\S 13$ (incluídas). Guía 1 de Ejercicios.
Certamen 1 (C1): Sábado 16 de mayo. Contenidos a evaluar: $\S 1$ a $\S 21$ (incluídas). Guía 2 de Ejercicios.
Quiz 2 (Q2): Viernes 12 de junio. Contenidos a evaluar: $\S 1$ a $\S 26$ (incluídas). Guía 3 de Ejercicios
Certamen 2 (C2): Sábado 20 de junio. Contenidos a evaluar: $\S 1$ a $\S 30$ (incluídas). Guía 4 de Ejercicios. Ver también: Un ejemplo
Quiz 3 (Q3): Viernes 31 de julio. Contenidos a evaluar: $\S 1$ a $\S 40$ (incluidas). Guía 5 de Ejercicios.
Certamen 3 (C3): Sábado 8 de agosto. Contenidos a evaluar: $\S 1$ a $\S 45$ (incluidas) + Problemas "Bonus": $\S 44$ a $\S 48$. Apunte sobre Formas Hermitianas (incluye ejercicios).
Examen (E): Miércoles 12 de agosto. Contenidos a evaluar: $\S 1$ a $\S 43$.

La nota final NF se calcula de acuerdo a la fórmula NF = 0.3 C1 + 0.1 Q1 + 0.25 C2 + 0.05 Q2 + 0.25 C3 + 0.05 Q3. Estudiantes cuya nota final sea estrictamente inferior a 55 y estrictamente superior a 40 tendrán derecho a un examen global (escrito), cuya ponderación será de 65%, para optar a aprobar MAT210 con nota 55. En caso de no aprobar el examen global, el estudiante mantendrá su nota final NF original. Explícitamente, la Nota Definitiva ND para quienes deban rendir el examen global se calcula de acuerdo a la fórmula: $$\mbox{ND}=\min\{55,\max(\mbox{NF},0.35\cdot \mbox{NF}+0.65\cdot \mbox{E})\}. $$

Clases (referencial) en Video y PDF

06/04/2020: Presentación del curso. Espacios vectoriales. Familias generadoras, libres, bases y dimensión (parte 1).
08/04/2020: Familias generadoras, libres, bases y dimensión (parte 2). Núcleo, imagen y teorema del rango. Aplicaciones lineales y matrices.
13/04/2020: Cambio de base. Operaciones elementales sobre filas y columnas (parte 1).
15/04/2020: Operaciones elementales sobre filas y columnas (parte 2). Polinomios de endomorfismos. Permutaciones. Formas multilineales alternadas (parte 1).
20/04/2020: Formas multilineales alternadas (parte 2). Definición de determinante. Determinante de un endomorfismo.
22/04/2020: Determinante de una matriz. Cálculo de determinantes.
27/04/2020: Valores y vectores propios. Endomorfismos diagonalizables.
29/04/2020: Polinomio característico de una matriz cuadrada. Polinomio característico de un endomorfismo. División de polinomios (parte 1).
04/05/2020: División de polinomios (parte 2). Trigonalización y Teorema de Cayley-Hamilton.
06/05/2020: Polinomio minimal. Reducción de endomorfismos y Descomposición de Dunford (parte 1).
11/05/2020: Reducción de endomorfismos y Descomposición de Dunford (parte 2).
13/05/2020: Reducción de endomorfismos y Descomposición de Dunford (parte 3). Cálculos de Descomposiciones de Dunford.
25/05/2020: Forma canónica de Jordan (parte 1).
27/05/2020: Forma canónica de Jordan (parte 2). Espacios vectoriales normados (parte 1).
01/06/2020: Espacios vectoriales normados (parte 2). Exponencial de matrices.
03/06/2020: Sistemas y EDO lineales con coeficientes constantes.
08/06/2020: Espacios vectoriales cocientes. Formas lineales y espacio dual (parte 1).
10/06/2020: Formas lineales y espacio dual (parte 2). Formas bilineales y formas cuadráticas.
15/06/2020: Ortogonalidad respecto a una forma cuadrática. Clasificación de formas cuadráticas reales y complejas.
17/06/2020: Método de reducción de Gauss. Grupo ortogonal. Producto escalar y espacios euclideanos (parte 1).
01/07/2020: Producto escalar y espacios euclideanos (parte 2). Bases ortonormales y ortogonalización de Gram-Schmidt (parte 1).
03/07/2020: Bases ortonormales y ortogonalización de Gram-Schmidt (parte 2). Endomorfismo adjunto y endomorfismos simétricos. (Clase recuperativa)
06/07/2020: Isometrías del plano y orientación. Isometrías del espacio (parte 1).
08/07/2020: Isometrías del espacio (parte 2). Isometrías en dimensión arbitraria y Teorema de Cartan-Dieudonné. Reducción simultanea de formas cuadráticas y cuádricas (parte 1).
22/07/2020: Reducción simultanea de formas cuadráticas y cuádricas (parte 2). Formas hermitianas. Teorema de Sylvester en el caso hermitiano y grupo unitario (parte 1).
24/07/2020: Teorema de Sylvester en el caso hermitiano y grupo unitario (parte 2). Producto escalar complejo y espacios hermitianos. (Clase recuperativa)
27/07/2020: Producto tensorial de espacios vectoriales.
29/07/2020: Álgebra tensorial. Álgebra exterior y formas multilineales alternadas (parte 1).
03/08/2020: Álgebra exterior y formas multilineales alternadas (parte 2).
05/08/2020: Pffafiano y matrices anti-simétricas. Álgebra simétrica y anillos de polinomios.

Errata

$\S 14$, Ejercicio$^*$ (página 29): "$\ker(\rho)=V_1\cap V_2$" debería ser $\ker(\rho)\cong V_1\cap V_2$. Esto último fue corregido en la Guía 2 de Ejercicios (Problema 2).
$\S 21$, Línea 9 (página 48): "$V_{({\lambda_j})}=\ker((u-\lambda_j\mbox{Id}_V)^1)=V_{({\lambda_j})}$" debería ser "$V_{({\lambda_j})}=\ker((u-\lambda_j\mbox{Id}_V)^1)=V_{\lambda_j}$" (es decir, el espacio característico $V_{({\lambda_j})}$ y el espacio propio $V_{\lambda_j}$ coinciden).
$\S 22$, Ejemplo 1 (línea 4, página 53): "$V_i=\operatorname{Vect}_\mathbb{C}\langle(1,i,-1,i)\rangle$" debería ser "$V_i=\operatorname{Vect}_\mathbb{C}\langle(1,i,-1,-i)\rangle$" (error de signo en la última coordenada; $V_{-i}=\overline{V_i}$ está correcto).
$\S 24$, Línea 18 (página 68): "$\displaystyle\sum_{\substack{i,j\geq 0 \\ i+j\leq m}}\|A_i\|_1\|V_j\|_1$" debería ser "$\displaystyle\sum_{\substack{i,j\geq 0 \\ i+j\leq m}}\|A_i\|_1\|B_j\|_1$".
$\S 25$ Observación (página 69): "$\operatorname{exp}\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}$" debería ser "$\operatorname{exp}\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$".
$\S 25$ Demostración del Lema útil (página 71): "$J_m^k e_i = \left\{\begin{array}{cl} 0 & \text{si }i=1,\ldots,k \\ e_{i-k} & \text{si }i=k+1,\ldots,d\end{array} \right.$" debería ser "$J_m^k e_i = \left\{\begin{array}{cl} 0 & \text{si }i=1,\ldots,k \\ e_{i-k} & \text{si }i=k+1,\ldots,m\end{array} \right.$ ".
$\S 26$ Demostración del Teorema, Línea 3 (página 75): "$Ae^{tA}X_0=AX'(t)$" debería ser "$Ae^{tA}X_0=AX(t)$".
$\S 28$ Demostración del Lema, Línea 1 (página 86): "$0=\left(\sum_{j=1}^n \lambda_j e_j^\ast \right)(e_k)=\sum_{j=1}^n \lambda_j e_j^\ast(e_k)=\lambda_j$" debería ser "$0=\left(\sum_{j=1}^n \lambda_j e_j^\ast \right)(e_k)=\sum_{j=1}^n \lambda_j e_j^\ast(e_k)=\lambda_k$".
$\S 38$ Demostración de Proposición, Línea 6 (página 118): "$V_1=\ker(u-\mbox{Id}_V)=L$ es una tal que $u|_L=\mbox{Id}_L$" debería ser "$V_1=\ker(u-\mbox{Id}_V)=L$ es una recta tal que $u|_L=\mbox{Id}_L$".
$\S 42$ Demostración de Proposición, Línea 2 (página 134): "$^t(AX)H\overline{AY}=\; ^tX(^tAH\overline{A})Y$" debería ser "$^t(AX)H\overline{AY}=\; ^tX(^tAH\overline{A})\overline{Y}$."
$\S 43$ Teorema (proyección ortogonal), ítem (3) (página 135): "$(U^\perp)^\perp$ y en particular (...)" debería ser "$(U^\perp)^\perp= U$ y en particular (...)".
$\S 44$ Ejemplo, Línea 7 (página 140): En la igualdad "$(x_1e_1+y_1e_2)\otimes (x_2e_1+y_2e_2)=x_1x_2 (e_1\otimes e_1)+x_1y_2 (e_1\otimes e_2)+x_2y_1(e_2\otimes e_1)+x_2y_2(e_2\otimes e_2)$" el coefiente que acompaña al tensor $e_2\otimes e_2$ debería ser $y_1y_2$. Sin embargo, para obtener la biyección deseada entre formas bilineales $B:V\times V \to \mathbb{R}$ y formas lineales $f:(V\otimes V)^\ast \to \mathbb{R}$ conviene considerar en su lugar la igualdad "$(x_1e_1+x_2e_2)\otimes (y_1e_1+y_2e_2)=x_1y_1 (e_1\otimes e_1)+x_1y_2 (e_1\otimes e_2)+x_2y_1(e_2\otimes e_1)+x_2y_2(e_2\otimes e_2)$" para obtener las mismas variables que en la forma $B$. Este cambio se debe a que $(V\otimes V)^\ast \cong V^\ast \otimes V^\ast$ y luego hay que transponer para obtener las coordenadas duales.
$\S 44$ Proposición (functorialidad), última línea (página 141): "$(f'\otimes g')\circ (f\otimes g)=(f'\circ f)\otimes (g\circ g')$" debería ser "$(f'\otimes g')\circ (f\otimes g)=(f'\circ f)\otimes (g'\circ g)$" (corregir el orden de $g$ y $g'$).
$\S 44$ Ejemplo (producto de Kronecker), Línea 11 (página 142): La definción del producto de Kronecker $A\otimes B=\left(\begin{array}{cc}a_{11}B & a_{12}B \\ a_{21}B & a_{22}B \end{array} \right)$ es correcta, pero al desarrollarlo hay un error de tipeo en el bloque $2\times 2$ ubicado abajo a la izquierda (los coeficientes $a_{12}$ deberían ser $a_{21}$).

Referencias

P. R. Halmos, Espacios vectoriales finito-dimensionales.

E. L. Lima, Álgebra linear.
O. Debarre, Algèbre 2ème année. Ver aquí para un glosario matemático de francés a inglés.

Información Práctica

Nos reuniremos todos los lunes de 8:00 a 9:30 en la Sala P-214 y todos los miércoles de 8:00 a 9:30 en la Sala M-303.

Humor

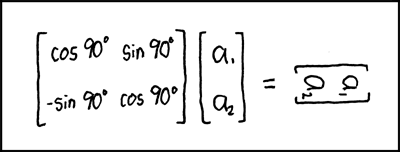
"Fijemos una orientación de un espacio euclideano $V\cong \mathbb{R}^n$ (...)"

Desafio

Un poco de álgebra no-lineal...

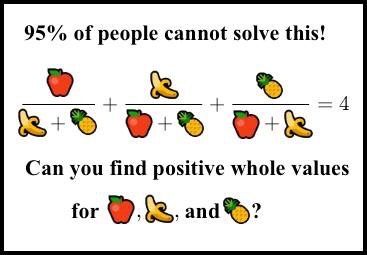
¡El 95% de las personas no puede resolver esto! (...) ¿Puedes encontrar todas las soluciones enteras positivas (i.e., soluciones en $\mathbb{N}^{\geq 1}$)? [Respuesta al final del curso]. Ver solución: aquí.